ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
CAHSEE Videos 392 videos
CAHSEE 1.2 Passage Drill. Which of these sentences from the story best illustrates the sensitive side of the narrator's nature?
CAHSEE 1.3 Passage Drill. Which of the following is the best way to express the meaning of the word alumni in this sentence?
CAHSEE 1.4 Passage Drill. What does the use of flashbacks accomplish in "Graduation"?
CAHSEE Math 1.5 Statistics, Data, and Probability I 234 Views
Share It!
Description:
Statistics, Data, and Probability I: Drill Set 1, Problem 5. Which should be used to represent her time?
- Statistics and Probability / Summarize, represent, and interpret data on a single variable
- Statistics and Probability / Summarize, represent, and interpret data on a single variable
- Statistics and Probability / Summarize, represent, and interpret data on a single variable
- Statistics and Probability / Summarize, represent, and interpret data on a single variable
- Statistics, Data Analysis, and Probability 6 / Statistical data
Transcript
- 00:03
Okay, let's get down to the shmoopy question.
- 00:06
Tamara, a runner in her high school track team, posted lap times of 24, 18, 21, 15,
- 00:13
and 18 seconds on her practice runs.
- 00:15
If her coach allowed her to pick the mean, median, or mode of this set for evaluation
- 00:20
of her fastest times, which should she use to represent her time?
Full Transcript
- 00:26
Here are the possible answers:
- 00:33
Clearly Tamara needs to work on her pacing.
- 00:35
Like... come on... a 15 second lap and a 24 seconder?
- 00:38
What is she... downing Big Macs between laps?
- 00:41
Okay... now what's this... semi-weird question asking?
- 00:44
Well, 3 things, really... all involving vocab words we have to know:
- 00:49
That's mean... median... and mode.
- 00:52
And there's a curve ball thrown in here...
- 00:54
in that we want the lowest number...
- 00:57
The lowest number represents the shortest time it took Tammy-pie to run her lap.
- 01:02
Smaller is better.
- 01:04
So there are 3 parts to this problem.
- 01:07
First, we calculate the mean or average... which is:
- 01:10
24 + 18 + 21 + 15 + 18, which totals 96.
- 01:15
Divide the 96 by 5, since we're averaging 5 elements...
- 01:19
...and we get 19.2 as the mean.
- 01:22
So Tamara's mean time based on this assessment of her fine athletic field efforts is 19.2.
- 01:27
We're a third of the way there. Second, we calculate the median.
- 01:31
Median is just a fancy way of saying "the middle."
- 01:34
Once we order the numbers from smallest to biggest...
- 01:38
...we can see that the middle number is 18.
- 01:41
So the median has beaten out the mean by 1.2 seconds.
- 01:45
But we have a third calculation we need to apply... mode.
- 01:49
In other words, what number occurs most frequently?
- 01:52
Doesn't matter how big it is. For example, if we're looking for the mode among 99,
- 01:56
98, 97, 96, 2 and 2...
- 01:58
Our mode is 2. Score one for the little guy. Right. So what's the mode here? 18.
- 02:05
It appears we have a tie.
- 02:07
Median and mode... going to sudden death...
- 02:09
So the answer is D, "either"...
- 02:12
...that is, the median and mode are both 18.
Related Videos
CAHSEE Math: Algebra and Functions Drill 5, Problem 3. Solve the equation.
Statistics, Data, and Probability I: Drill Set 3, Problem 4. How many different avatars can be created based on the given options?
Statistics, Data, and Probability II Drill 3 Problem 2. Which two sports together make up for the preferences of more than half of all those w...
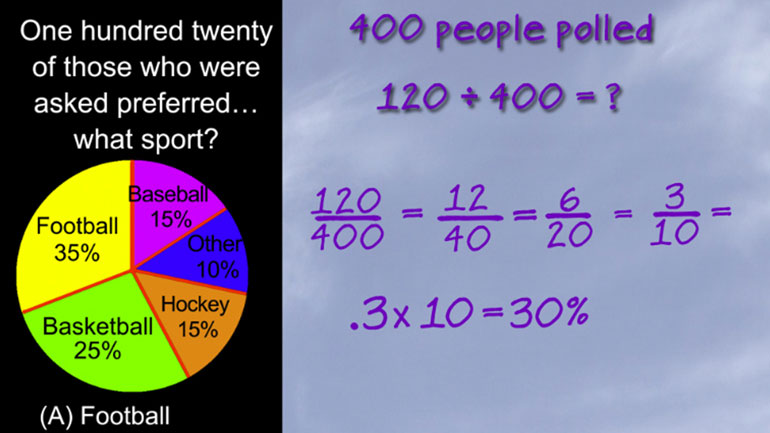
Statistics, Data, and Probability II Drill 3 Problem 3. One hundred twenty of those who were asked preferred what sport?