Answer
The region looks like this:
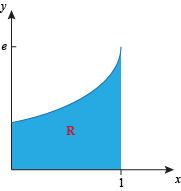
and the solid looks like this:
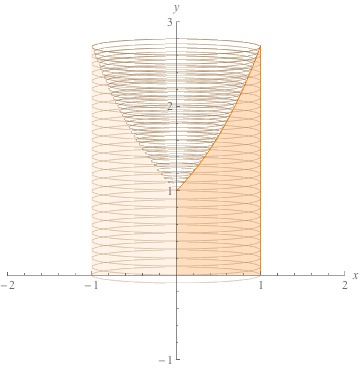
(a) If we try to use the washer method, we have to deal with the solid in two separate pieces. From y = 0 to y = 1, all slices perpendicular to the y-axis are disks of radius 1. The volume of this part of the solid is
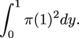
From y = 1 to y = e, slices perpendicular to the y-axis are washers with outer radius 1 and inner radius x = ln y.
The volume of this part of the solid is
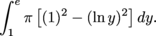
To get the volume of the entire solid, we add the volumes of its two pieces:
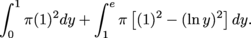
(b) If we use the shell method we can deal with the whole solid at once. The cylinder at position x has radius x and height y = ex. The volume of the solid is
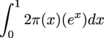
The two different methods will give the same answer. We definitely prefer the shell method here, though. Less steps equals less work.