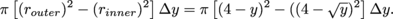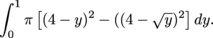We're getting pretty familiar with this region by now: 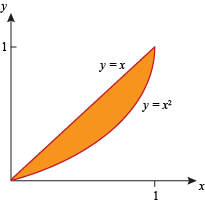
(a) When we rotate R around the line y = -1, we get a solid with a hole in its middle. This means a slice of this solid will look like a washer. The outside of the solid is bounded by the line y = x. However, since the center axis of the solid is not the x-axis, the outer radius is not just x. If we look at the picture we can see that the outer radius is router = x + 1. Similarly, the inside of the solid is bounded by the line y = x2. Since the center axis of the solid is at y = -1, which is a distance of 1 away from the x-axis, we have to add 1 to get the inner radius rinner = x2 + 1. We have router = x + 1 and rinner = x2 + 1, so the volume of the washer is π[(router)2 – (rinner)2] Δ x = π [(x + 1)2 – (x2 + 1)2 ] Δ x. The variable x goes from 0 to 1 in the region, so the volume of the solid is 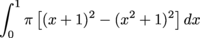
(b) When we rotate R around the line x = 4 we get the solid 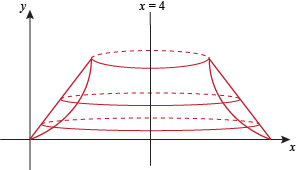
Slices perpendicular to the line x = 4 are washers. The outer boundary of the solid is at the line y = x. However, the center line of the solid is at x = 4. By looking at the picture we can see that the outer radius of the slice at height y is router = 4 – x = 4 – y. The inner boundary of the solid is the line y = x2, or  . By looking at the picture, we can see that the inner radius of the slice at height y is . By looking at the picture, we can see that the inner radius of the slice at height y is  . . The volume of the slice is 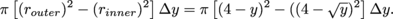
The variable y goes from 0 to 1 in the original region R, so the volume of the solid is 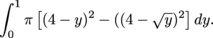
We're being bombarded with a multitude of pitched frisbee disks because it's important. Even the most experienced volume-making, cake baking, frisbee tossing expert draws pictures to avoid making mistakes. | 



 .
.


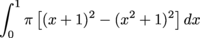

 . By looking at the picture, we can see that the inner radius of the slice at height y is
. By looking at the picture, we can see that the inner radius of the slice at height y is  .
.