ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Measurement (Linear, Area, Three-Dimensional) Videos 10 videos
A cardboard box measures 12 inches wide, 8 inches across, and 6 inches tall. What is its volume in cubic feet?
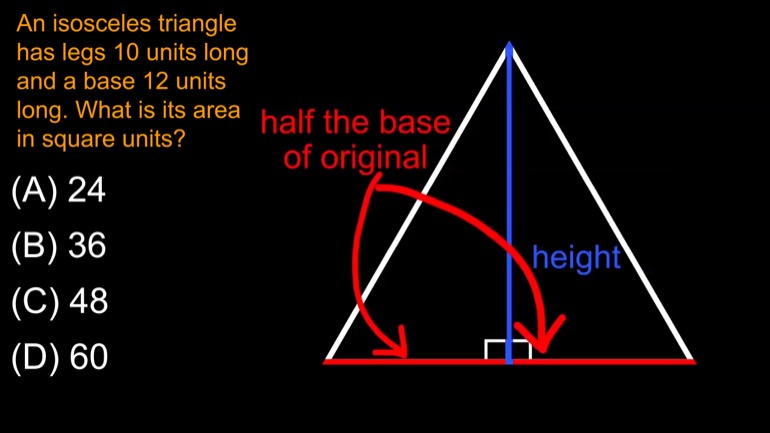
An isosceles triangle has legs 10 units long and a base 12 units long. What is its area in square units?
A circle has an area of 225π square units. What is its circumference?
TSI Math: Solving for a Triangle's Area Using the Pythagorean Theorem 13 Views
Share It!
Description:
An isosceles triangle has legs 10 units long and a base 12 units long. What is its area in square units?
Transcript
- 00:02
All right sy mash my uppers next up and i
- 00:04
saw seles Triangle has legs thes things Ten units long
- 00:09
in a base Twelve units long What is its area
- 00:12
in square units All right Well let's See No reason
- 00:18
if you're triangles When in doubt draw a diagram The
Full Transcript
- 00:21
area the triangles one half the base times the height
- 00:24
In this situation we need to find height Well if
- 00:26
we imagine cutting the given triangle in half to form
- 00:29
two right triangles like this one here the height is
- 00:32
the vertical leg of each right triangle Well the horizontal
- 00:36
leg of each right triangle is half the base of
- 00:39
the original triangle Because of the whole cutting in half
- 00:42
thing they're so here check it out Looks like this
- 00:44
Get the ten thing in the ten thing in the
- 00:46
six there in the h there which is right Well
- 00:48
we'll use the pythagorean theorem to find age And yes
- 00:51
it was his best serum by far So we've got
- 00:54
a squared plus b squared c squared or six squared
- 00:56
Plus h squared is ten square Now simplify it That
- 00:59
gives us thirty six Plus h squared is one hundred
- 01:02
subtract thirty six from both sides We get sixty for
- 01:06
eight square to sixty four square to sixty four is
- 01:09
eight So the triangle is eight units tall in the
- 01:12
area of the original triangle then is one half base
- 01:16
times height right So it's a halftime twelve times eh
- 01:19
which is six times eight or forty eight square units
- 01:23
and note that we use the full base of the
- 01:25
original triangle there Twelve So that's it The answer is 00:01:29.552 --> [endTime] c forty eight or shmoop Uh
Related Videos
Which is the best way to revise and combine sentences 1 and 2?
Where would the following sentence best be placed?
Which of the following is best to insert at the beginning of sentence 8?
Which is the best location for sentence 9?
Which of the following sentences is best to insert between sentences 11 and 12?