ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Algebra and Functions Videos 140 videos
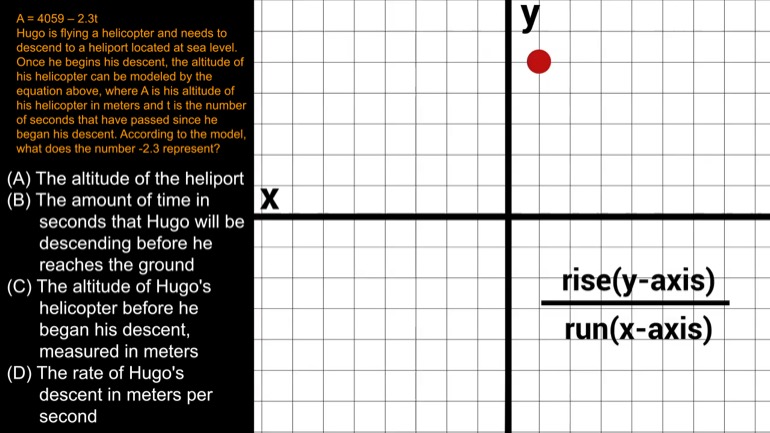
SAT Math 2.3 Algebra and Functions. Calculate this function.
SAT Math: Calculating Heating Time Using Proportion and Equations 7 Views
Share It!
Description:
When placed in a glass beaker on a hot plate at a moderate temperature, 5 milliliters of water heats up at a rate of 8 °C per second. The amount of time it takes to heat water increases linearly when heating greater amounts of water. Eduardo needs to boil 300 milliliters of water for a chemistry experiment. How many minutes would he need to wait for the water to reach its boiling point of 100 °C, given that the water's initial temperature is 25°C? Round your answer to the nearest tenth.
Transcript
- 00:01
Arch members knew section same grid thing here with the
- 00:06
circles squares and triangles in the little dunce cap here
- 00:09
right at the bottom I used to wear that a
- 00:11
lot All right here we go men Last play at
- 00:14
a moderate temperature Five milliliters water heats up at a
Full Transcript
- 00:16
rate of degrees centigrade for second amount of time It
- 00:18
takes to keep water increases linearly when he'd in greater
- 00:19
amount of water and water With these guys you're about
- 00:21
one hundred meters of water for chemistry That's What you
- 00:23
need to wait for the water to reach it's boiling
- 00:24
point one hundred grand larceny attempted to raise your answer
- 00:26
in your hand right We're going up seventy five degrees
- 00:30
here from twenty five to one hundred boiling point and
- 00:33
it's increasing at eight degrees centigrade per second Arithmetically Meaning
- 00:37
steadily not geometrically or some other weird combo thing So
- 00:41
how do we think about this Well if you're not
- 00:43
a science fan pour you pretend that eduardo is actually
- 00:46
trying to make soup or coffee or whatever parade for
- 00:49
practice still applications Yet you too could be a barista
- 00:52
someday five milliliters of water rises eight degrees centigrade in
- 00:55
one second Since the problems says that heating time increases
- 01:00
leaning yearly with greater amounts of water While set up
- 01:03
a proportion to see how long it takes for three
- 01:05
hundred milliliters they heat up eight degrees centigrade it right
- 01:08
We have five milliliters is one second So three hundred
- 01:11
millilitres is how many seconds Well yeah It's a minute
- 01:13
Right Five over One three hundred over x Yeah The
- 01:16
expression tells us that three hundred million litres of water
- 01:18
heats up eight degrees centigrade in sixty seconds What a
- 01:21
convenient cohen kid ink Sixty seconds is one minute and
- 01:24
the problem wants the answer in minutes Who Who We
- 01:27
can say that two Hundred million litres of water heats
- 01:29
at eight degrees per minute Now we need to cook
- 01:32
up an equation to see how long it takes to
- 01:34
cook up the water Well the water temperature rises at
- 01:36
eight degrees centigrade a minute So this value is the
- 01:39
slope right there that represent the final temperature is sea
- 01:42
in the number of minutes of eating time is t
- 01:45
so c equals eight t one more thing The water's
- 01:48
already at twenty five degrees If it were zero well
- 01:51
we'd be playing around with ice Great for a hot
- 01:54
summer day Not great for a problem like this to
- 01:57
account for the water's initial temperature at twenty five is
- 01:59
the why in earth except in the equation Yeah just
- 02:02
c equals eighty plus twenty five hundred that's are boiling
- 02:06
point Their equals eighty plus twenty five track t from
- 02:10
outside to get seventy five equals eighteen Divide ate both
- 02:13
sides And while you get about nine point four Well
- 02:15
eduardo needs to wait nine point four minutes for that
- 02:18
soup or coffee or chemistry experiment Tio a boil Maybe
- 02:22
he can boil some tea while he waits Yeah Put
- 02:24
that hot water to use
Related Videos
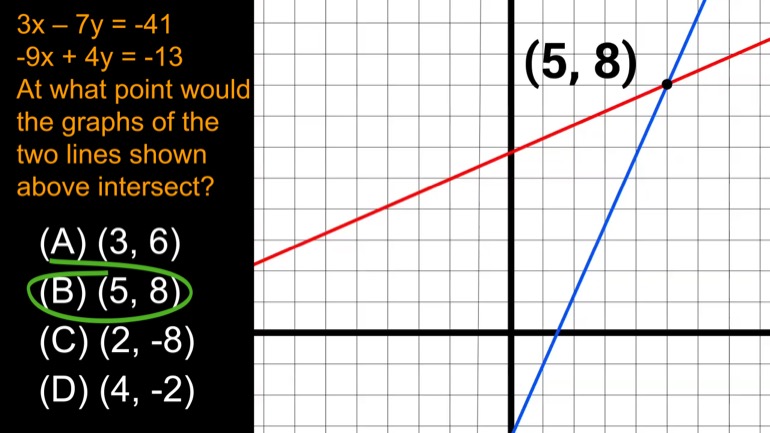
SAT Math 1.1 Algebra and Functions. Find an algebraic equation to correspond with the data.
SAT Math 1.1 Geometry and Measurement. What is the circumference of the circle?
SAT Math 1.1 Numbers and Operations. How many combinations of beverage and cereal can be made?
SAT Math 1.1 Statistics and Probability. In which of the following data sets are the arithmetic mean and the median equal?
SAT Math: Algebra and Functions Drill 1, Problem 2. Based on the data in the table, what is the maximum heart rate for the average 22-year-old?