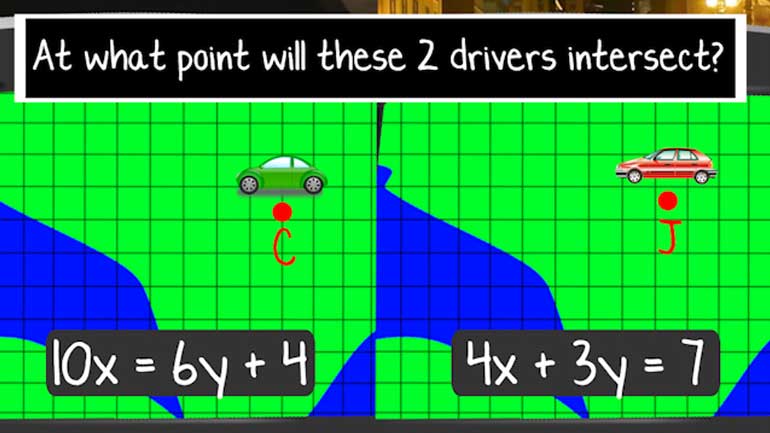
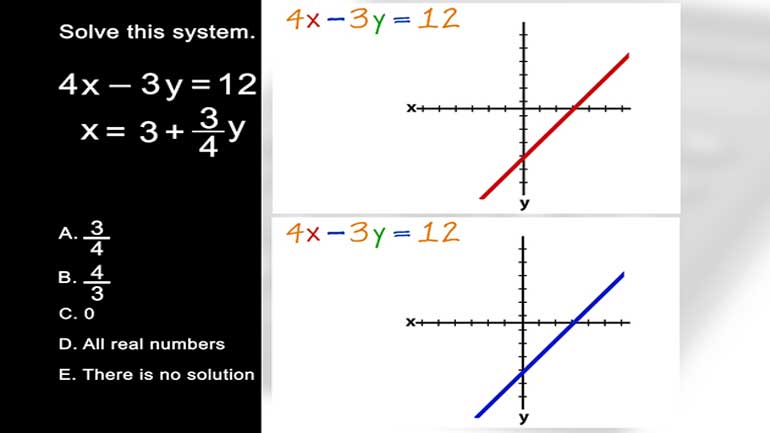
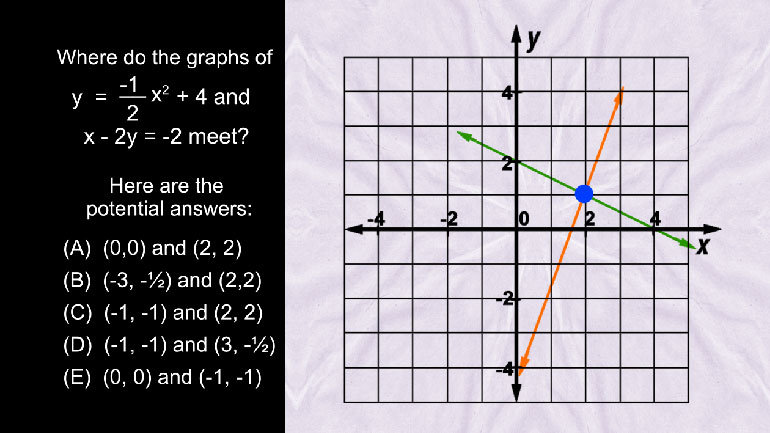
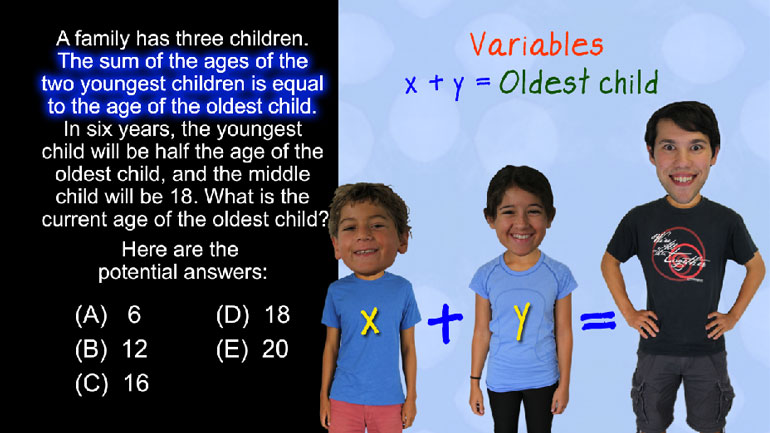ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Systems of Equations Videos 73 videos
How do you solve a system of linear inequalities? Aw, man...and we thought solving a problem like Maria was tough...
Please note: If starting your own petting zoo, Shmoop recommends you stock it with animals that aren’t quite so likely to bite your hand off. Tha...
SAT Math 1.1 Algebra and Functions 315 Views
Share It!
Description:
SAT Math 1.1 Algebra and Functions. Find an algebraic equation to correspond with the data.
Transcript
- 00:02
And we're getting mathy with it.
- 00:04
The table below gives the average maximum heart rate, by age, for a person exercising at full effort.
- 00:10
(Heart rate is in beats/min.)
- 00:13
Find an algebraic equation to correspond with the data.
- 00:16
Use a for age and h for heart rate.
Full Transcript
- 00:19
And here are your possible answers...
- 00:23
Okay, if we look at the data…
- 00:25
as age increases by 5, average max heart rate decreases by 5.
- 00:31
Since age acts as our independent variable and average max heart rate acts as our dependent variable,
- 00:42
we can calculate the change in average heart rate over age as the slope of our equation.
- 00:48
Which gives us negative 1. That's the slope.
- 00:51
The point slope form of a linear equation is y minus y1 equals slope times x minus x1.
- 00:58
And you should get that there are 2 points we’re thinking through here…
- 01:01
...that’s (x, y) and (x1, y1). h is y in this situation because it's the
- 01:06
dependent variable, and a is x in this situation because it's the independent variable.
- 01:12
We can take any x1 and y1 points... so let's just take the points 20 and 200.
- 01:18
Plugging into the equation with these numbers then, we get... h - 200 = -1(a - 20).
- 01:25
h minus 200 equals negative a plus 20.
- 01:28
Adding 220 to both sides of the equation... we have h equals 220 minus a.
- 01:34
Let's make sure this equation checks out with the data in the table....
- 01:37
Let’s plug in age 45 and see if the end answer is right.
- 01:42
Plugging in a equals 45...
- 01:44
h = 220 - 45, so that's 175.
- 01:49
Check it here on the table and yup, it checks out!
- 01:51
So our equation is h equals 220 minus a.
- 01:56
Answer A is our guy!
Related Videos
SAT Math 2.1 Geometry and Measurement. What is the measure of angle z in terms of x and y?
In 2014, the unemployment rate of one county in California was 7%. In another county, the unemployment rate was 11%. Which of the following express...
Angela is making cookies for a bake sale. She expects each batch of her cookies to sell for $40. It costs her $10 to make one batch of cookies, and...