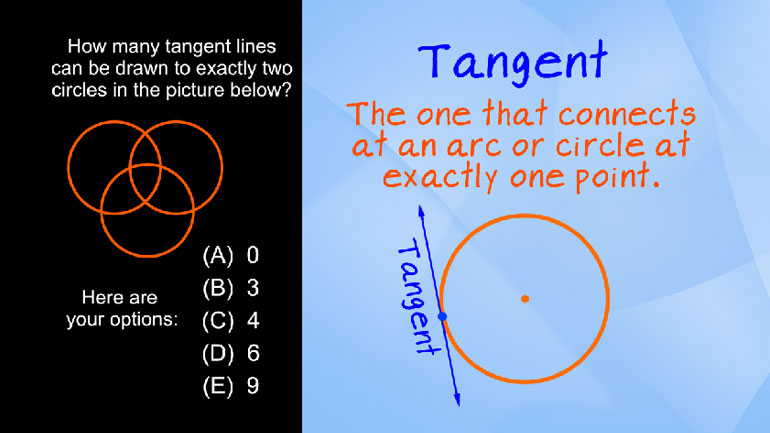
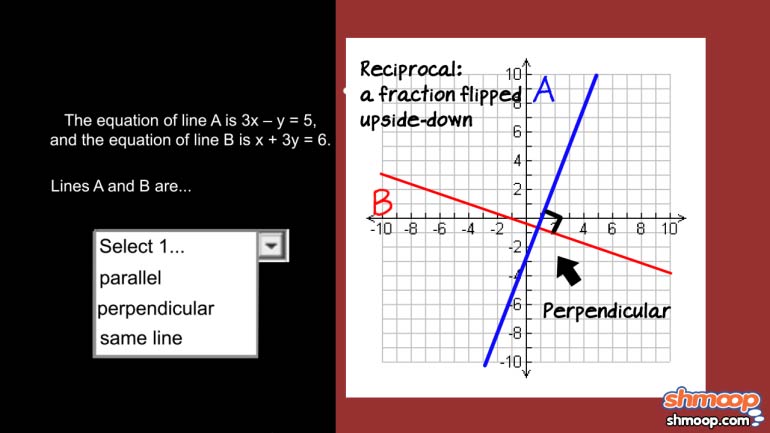
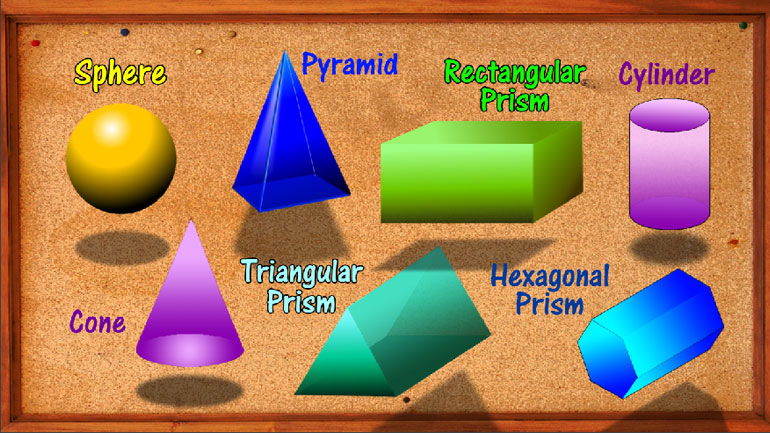
ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Parallel and Perpendicular Lines Videos 23 videos
This video explores parallel lines and transversals: how to identify them both on a math test and in real life urban planning. What do the consecut...
To prove lines are parallel, you need a third line. We at Shmoop (and the rest of the world) call it a transversal.
Parallel Lines and Transversals 34138 Views
Share It!
Description:
This video explores parallel lines and transversals: how to identify them both on a math test and in real life urban planning. What do the consecutive interior angles tell us? What about the corresponding angles? How can we tell if two lines are parallel to each other?
Transcript
- 00:06
Parallel Lines, Transversals, and Angles, a la Shmoop.
- 00:09
There are some couples who are just destined to be together forever.
- 00:12
Romeo and Juliet. Cinderella and Prince Charming. Paula Deen and butter.
- 00:18
But the greatest couple of them all has to be…
- 00:21
…parallel lines. Parallel lines never touch, but they always
Full Transcript
- 00:25
stand by their partner. They stay by each other's sides forever. That's love.
- 00:30
Besides, it's more romantic than having one wild encounter and then parting ways afterwards.
- 00:34
When a transversal cuts across two parallel lines, it forms eight angles.
- 00:36
If the measure of angle 1 is 110 degrees, what are the measures of the other 7 angles?
- 00:39
Sounds like a lot of work, but it's not as bad as you might think.
- 00:43
First, we can see that angles 1 and 3 are vertical angles, and we know that vertical
- 00:48
angles are always congruent… in other words, they have equal measurements.
- 00:50
So angle 3 has a measure of 110 degrees, too.
- 00:53
It also helps to know that corresponding angles…
- 00:55
…or angles that are in the same position relative to the parallel lines and the transversal…
- 00:57
…are also congruent.
- 00:57
In this case, the corresponding angle to angle 1 is angle 5…
- 00:59
…because it's above the parallel line and to the left of the transversal. So angle 5
- 01:02
is also 110 degrees. Wait. So angles 3 and 5 are congruent, too?
- 01:03
Actually… yes.
- 01:03
They're both on the interior between the two parallel lines and on alternate sides of the
- 01:06
transversal, so we call them alternate interior angles.
- 01:06
All alternate interior angles are congruent. There's one more angle that's 110 degrees,
- 01:09
and that's angle 7.
- 01:09
Angle 1 and angle 7 are both on the exterior of the parallel lines and alternate sides
- 01:11
of the transversal, so they're called alternate exterior angles.
- 01:13
Alternate exterior angles are also congruent, and we can check that using vertical angles
- 01:16
or corresponding angles.
- 01:16
Yup, looks like 110 degrees to us. Those are all the odd angles, but what about
- 01:20
the evens? We know that a straight angle, or a line,
- 01:22
has 180 degrees.
- 01:22
Since any even angle makes a linear pair with an odd angle, any even angle is supplementary
- 01:24
to an odd angle.
- 01:25
That means the even angles have a measure of 180 minus 110… or 70 degrees.
- 01:26
And ta-da! You now have all your angles. So don’t forget to include parallel lines
- 01:29
when listing the world’s great love stories.
- 01:29
And as a bonus tip… don’t ever try to get between Paula Deen and her butter.
Related Videos
Haven't you always wondered how much cardboard it takes to encase a trunk warmer for your pet elephant?
Want to figure out the area and perimeter of irregular shapes? Break them down into regular shapes. For example, a flower can be broken down into s...
It's one thing when all those shapes are sitting flat on the page. But when they start popping out and invading our personal space bubble, we get a...
Does thinking about 3D Geometry get you bent out of shape? Never fear! Watch this video and figure out some fun new shapes to bend back into. We're...
ACT Math: Plane Geometry Drill 3, Problem 5. How long would it take for the wheel to make two rotations?