ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Ratios, Percentages, and Proportions Videos 55 videos
SAT Math 10.3 Geometry and Measurement. What is the ratio of birds to dogs?
SAT Math 2.1 Statistics and Probability. Which two items have the highest protein to fat ratio?
SAT Math 2.2 Statistics and Probability. What percent of her recommended daily intake of 2000 calories did she consume?
Math Basics: Similar Figures 1001 Views
Share It!
Description:
This video explains similar figures and how to figure out if two shapes are similar using sides and angles. Plus, it discusses how to use one shape figure out unknown measurements of a similar shape.
Transcript
- 00:04
Similar Figures, a la Shmoop.
- 00:07
We here at Shmoop have been making great strides on our new shrink ray design. [Girls working at shmoop]
- 00:12
We just have to…work out a few final kinks.
- 00:15
But it sure has taught us a lot about similar figures…
- 00:18
…which are figures that have the same shape
Full Transcript
- 00:20
as one another, but not necessarily the same size. [Two different size cubes spin]
- 00:24
Let’s take the Bermuda Triangle, for example. It’s rumored that any ship that sails into [Ship sailing into the bermuda triangle]
- 00:29
this part of the ocean…instantly sinks.
- 00:32
Now let’s say the Bermuda Triangle is twenty miles by twelve miles by eight miles.
- 00:38
And in order for his cousin, “Little” Bermuda Triangle, to be a similar figure…
- 00:42
…she would have to have the same exact proportions. [Two different size triangles]
- 00:45
If each side of the little Bermuda Triangle is exactly proportional to the corresponding
- 00:51
side of the real Bermuda triangle… …the two triangles would be similar figures.
- 00:56
So…if Little Bermuda is 10 by 6 by 4…the triangles would be similar…
- 01:01
…since each distance is exactly half that of the original.
- 01:05
If Little Bermuda is ten by six by two… …then our hopes are sunk. [Hope sinks into ocean]
- 01:10
Because while two of the three sides are half the length of the original…
- 01:13
…the final side is only a quarter of the distance of its big cousin.
- 01:17
Another way to determine whether or not figures are similar is to check their angles. [Shape with legs dancing]
- 01:22
Ahem, said angles people, listen up.
- 01:25
If all of the corresponding angles in two triangles are the same, then the figures are similar.
- 01:29
Like…if this 35 degree angle matches this 35 degree angle… [Two 35 degree angle triangles]
- 01:33
…and this 45 degree angle matches this 45 degree angle…
- 01:36
…and this 100 degree angle matches this 100 degree angle.
- 01:40
Boom. Similar.
- 01:41
So we know that similar figures have sides that are proportionate and angles that are congruent.
- 01:47
Why might you need to pop this information into your brain? [Zombie man appears]
- 01:50
Say someday you become an architect, and you’d [Architect making measurements]
- 01:53
like to build a model of a proposed structure that isn’t, um…life-size.
- 01:57
That would be an awful waste of Styrofoam.
- 01:59
Now let’s say you want to know how tall an existing building is. [A tall skyscraper]
- 02:03
Maybe you need this information to rappel down the side of some building…
- 02:06
we won’t get too nosy.
- 02:08
Well, you can measure your own shadow. You know how tall you are, right? [Man stood measuring his shadow]
- 02:12
Now you can measure the building’s shadow. The proportion of actual height to the length [Man stood beside skyscraper]
- 02:17
of its shadow will be the same for you as for the building.
- 02:20
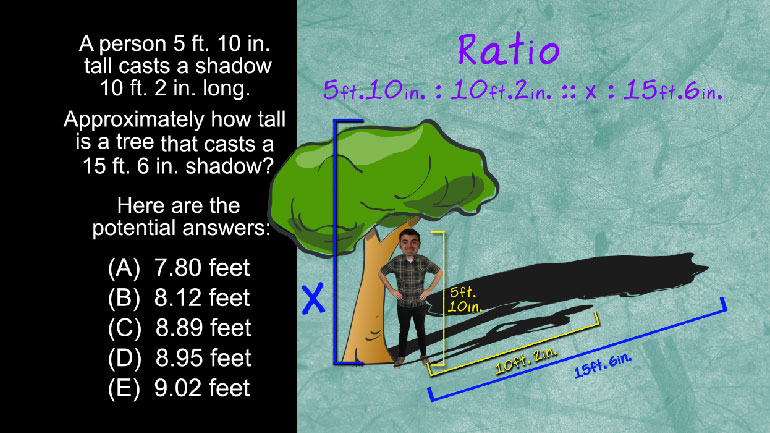
So…if you cast a three foot long shadow, and you’re six feet tall… looks like the
- 02:24
ratio is 2 to 1. So if the building casts a twenty foot long
- 02:28
shadow…the building must be forty feet high. Same ratio – 2 to 1.
- 02:34
If we look at these as triangles, we can see that we’re dealing with right angles…
- 02:38
…and as object and shadow height increase, so does the imaginary hypotenuse. [Man and skyscraper with 90 degree triangles in front of them]
- 02:44
It’s really just two similar triangles…and we can be sure that our determination of the
- 02:47
building’s height is accurate.
- 02:50
You may now rappel down it with complete confidence. Good luck avoiding the searchlights though… [Man rappelling down a skyscraper]
Related Videos
This video covers the different types of triangle. What makes a triangle isosceles, scalene, or equilateral? What about the different kinds of angl...
Sine is the opposite over the hypotenuse; cosine is the adjacent over the hypotenuse; and tangent is the opposite side over the adjacent side....
Someday you might be a big, fancy defense lawyer, and you'll have to prove that your client's triangle was congruent to the triangle in question. W...
You might not think that the properties of a triangle would be particularly helpful in the realm of Tootsie Pop lickology. But boy, would you be wr...
How does learning about triangle angles and types of triangles while being told a story about Goldilocks sound to you? Not too shabby. Grab a snack...