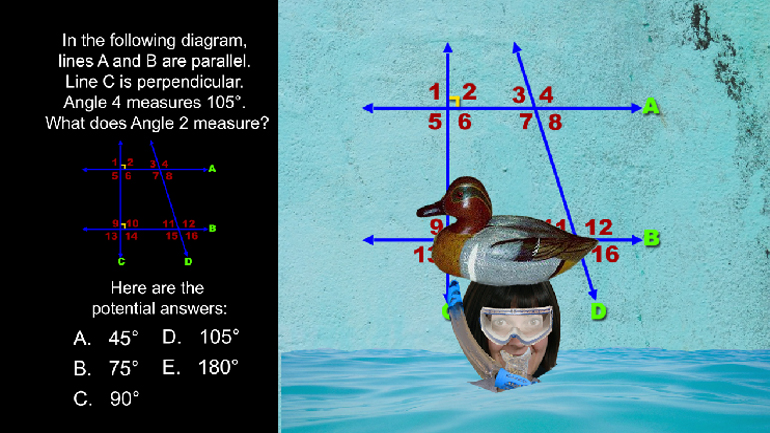
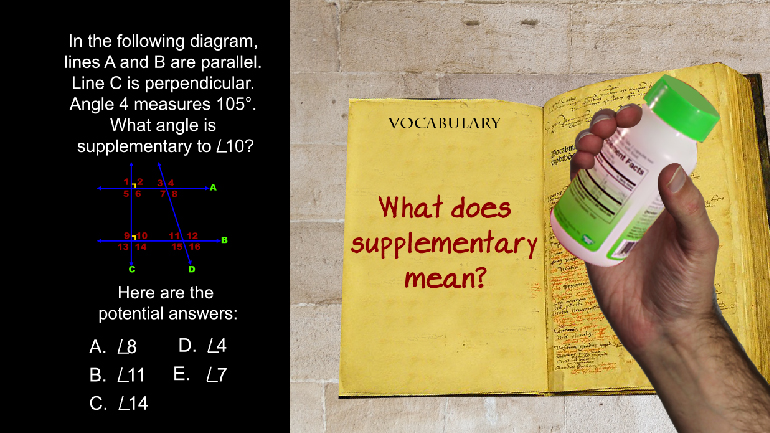
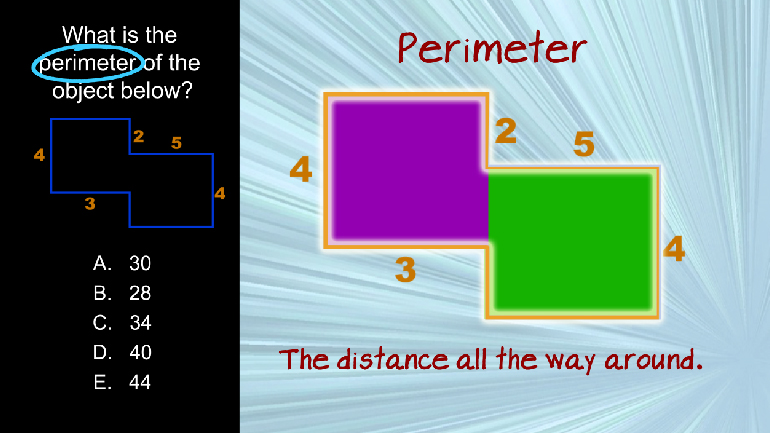
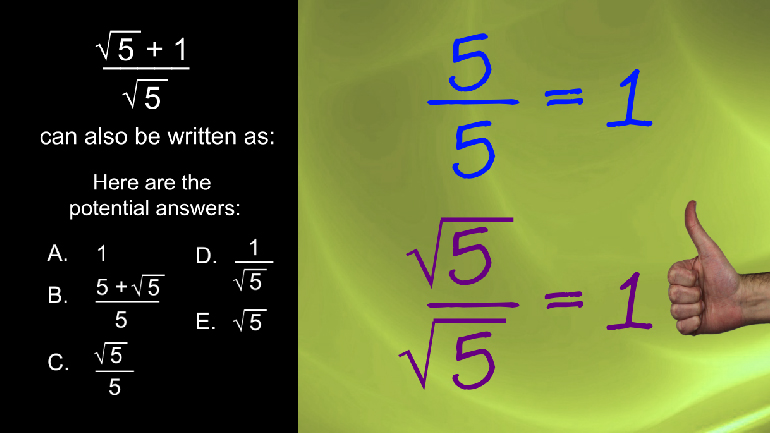ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
ACT Math Videos 161 videos
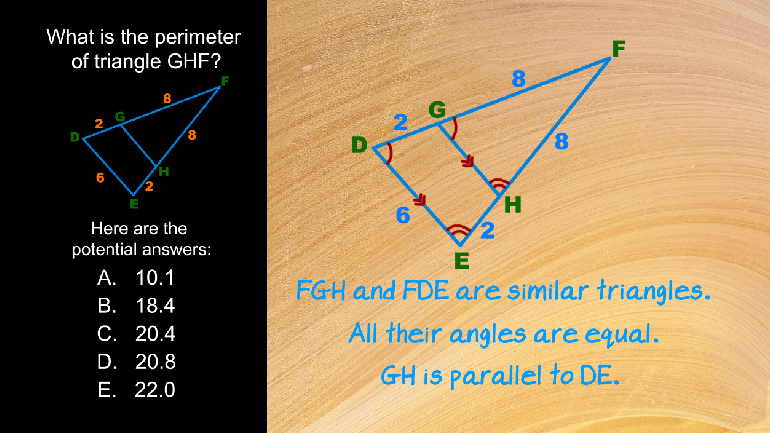
ACT Math: Plane Geometry Drill 3, Problem 1. What is the area of the trapezoid shape in the video?
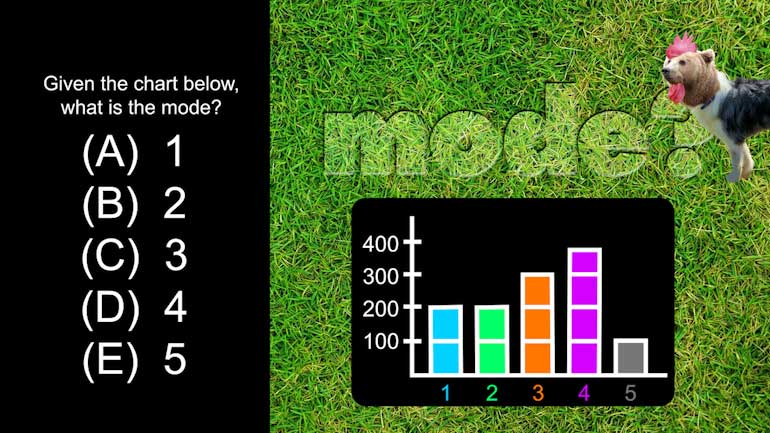
ACT Math Pre-Algebra Drill 2, Problem 5. Given the chart in the video, what is the mode?
ACT Math 5.1 Elementary Algebra 263 Views
Share It!
Description:
ACT Math: Elementary Algebra Drill 5, Problem 1. How old is Jeremy's brother?
Transcript
- 00:03
A little birdie told us you wanted to solve a shmoopy math problem...
- 00:07
Jeremy is one year older than twice his brother's age.
- 00:11
If Jeremy is 17, how old is his brother? And why don't we get to know his name?
- 00:19
And here are the potential answers...
- 00:23
First of all, don't get hung up on the fact
Full Transcript
- 00:25
that we don't get to find out Jeremy's brother's name.
- 00:27
With short problems like this, it's a good idea not to get too attached to the characters.
- 00:32
OK so what is this question asking?
- 00:34
It wants us to translate English into...Mathlish.
- 00:38
So here we go:
- 00:40
Jeremy equals 1 plus the quantity 2 times his brother's age.
- 00:44
And we know that Jeremy is 17.
- 00:46
So we substitute 17 for J and get 17 equals 1 plus 2b.
- 00:53
Subtract 1 from both sides and we have 16 equals 2b.
- 00:57
Divide both sides by 2 and we get... 8.
- 01:00
Answer A.
- 01:01
Now take a second to say good-bye to Jeremy's brother. You won't be seeing him again.
Related Videos
ACT Math: Plane Geometry Drill 3, Problem 1. What is the area of the trapezoid shape in the video?
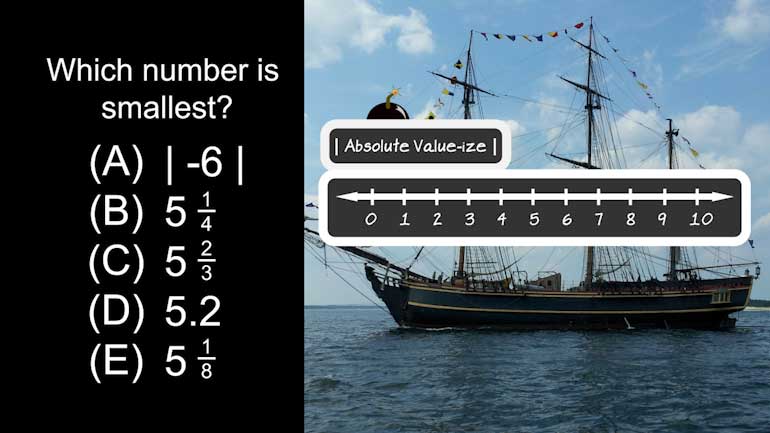
ACT Math: Coordinate Geometry Drill 1, Problem 1. Which inequality is expressed by the number line?
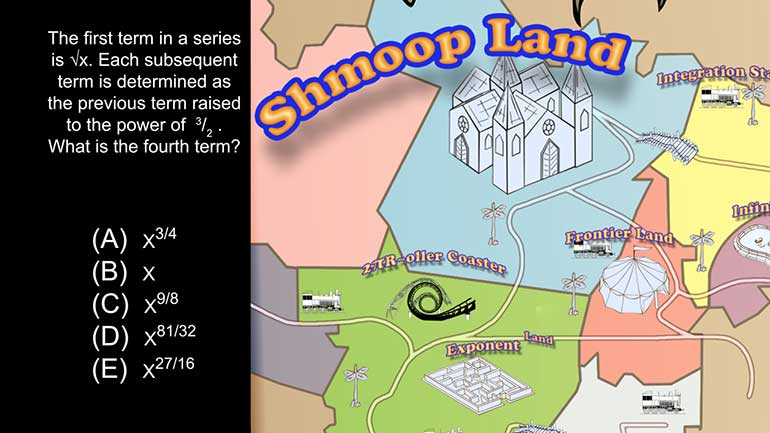
ACT Math: Intermediate Algebra: Drill 3, Problem 1. Find the fifth number in the series.
We don't like knocking people down to size, but we do like simplifying radicals. Join us?
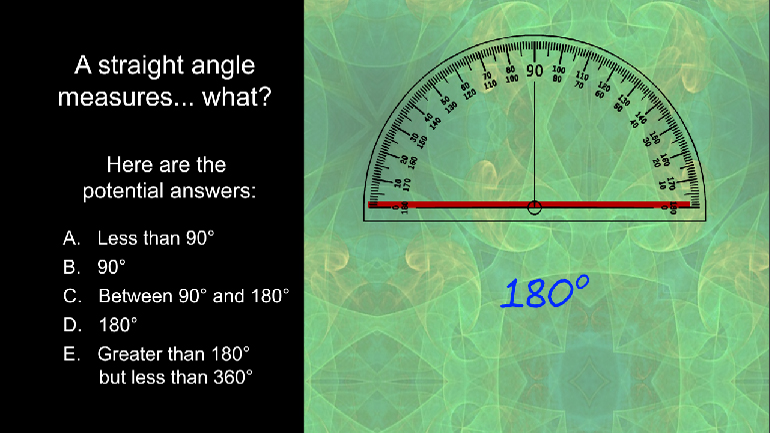
If fleeing criminals always fled the scene of the crime at perfect right angles, it would be much easier to determine their whereabouts. Fortunatel...