Properties of Exponents and Logarithms at a Glance

It's time for our master-class before facing off with Expo and his minions. Log sends us off to an old, musty library with stack after stack of books. They've got titles like Ye Olde Mathematical Beasts and Logarithmica Adeptus. Whenever you open up one of the ancient books, dust puffs out all over your face. Don't sneeze, though; that'll just stir it up even more.

Looking through them, you find some magical properties of logarithms and exponents. Some you've already met; some are fresh and new.

Sum of Logs:

log_b xy = log_b x + log_b y

For all of these properties, thinking about them in their exponential form is a big help. Remember that multiplying two numbers with the same base together means we add their exponents. For example, b^xb^y = b^{x + y}.

Difference of Logs:

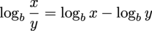
This one is similar to the previous property, but in reverse gear. If two numbers with the same base are divided, their exponents are subtracted from each other.

Exponent in Log:

log_b xⁿ = n log_b x

Whoa, how'd that exponent just decide to go outside the log? Expo just doesn't care 'bout anyone now, it seems. Zip, zoom, fly—it's time for exponent mode. Imagine the following situation:

10² = 100

If we cube each side, this is what would go down:

(10²)³ = 100³

The power of 3 on the right side is like n in the "exponent in log" rule. All you need to remember here is that when you raise an exponent to another exponent, you can multiply them:

10^{2 × 3} = 100³
10⁶ = 100³

Important note: we can only pull out the exponent from a log when it's attached to the entire expression inside the log. For example, we can turn log(3x)² into 2log(3x). But we can't do anything with log(3x²), because the exponent is only attached to the x, not the 3.

Log of 1:

log_b 1 = 0

Essentially all this property says is, "What exponent do we raise a base to so we get an answer of 1?" That only leaves one answer: 0. Absolutely any base raised to the power of 0 is 1. The base could be 1,000,000, but raising it to the 0 power would still give us 1. How mystical.

Equal Base:

log_b b = 1

Again, let's put on our exponential-form goggles. (Now you look like you're on a secret mission. So classy.)

The logarithm answers the question, "What's the exponent?" If we need the two sides to equal, the only exponent that would give a correct answer would be 1. It'd work out just to be b¹ = b.

Sample Problem

Demonstrate the sum of logs by expanding log 100 and solving, then demonstrate the exponent in log property by expanding.

There are two other ways to represent log 100: log(10 × 10) or log(10²).

If we expand the first way using the sum of logs rule, we get:

log(10 × 10) = log 10 + log 10 = 1 + 1 = 2

Solving log 100 the regular way also gives us 2 (remember, the common log has an invisible base of 10):

log 100 = x

10^x = 100

x = 2

If we expand the second way using the exponent in log rule, we get:

log(10²) = 2 log 10 = 2 × 1 = 2

No sweat.

Sample Problem

Simplify the following equation using the properties you've learned so far:

3log₄(16x⁵)

First let's pull that exponent down from its pedestal:

3(5)log₄(16x) = 15log₄(16x)

Then use the sum of logs rule to pull the logs apart, making sure to hold onto the coefficient:

15(log₄ 16 + log₄ x) = 15 log₄ 16 + 15 log₄ x

Simplify the first log, because 4² = 16:

15(2) + 15 log₄ x = 30 + 15 log₄ x

There's your answer. We can't simplify any further.

Sample Problem

Rewrite the following logarithmic equation into a single log, simplifying where possible, using the properties you've learned.

y = 0.5log₅(x²) + log₅(25x) – 1 – log₅ 5

Whoa boy. That's a Moby Dick-sized whale of a problem.

Let's go from left to right. First, pull the exponent out of the left log:

0.5log₅(x²) = 0.5(2) log₅ x = log₅ x

Split the middle log into a sum:

log₅(25x) = log₅ 25 + log₅ x = 2 + log₅ x

And simplify that log on the right:

log₅ 5 = 1

Let's see what we have left:

y = log₅ x + 2 + log₅ x – 1 – 1

y = log₅ x + log₅ x

Now we can reverse the sum of logs rule and combine these into a single log:

y = log₅(xx)

y = log₅ x²

One more round of pulling the exponent outta the log:

y = 2 log₅ x

Now that you've got all the skills to beat Expo at his own game, taking him down should be a cinch.