Answer
(a) Since 
on (0,1] and
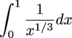
converges, so does
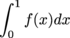
(b) Since 
on [1,∞) and
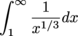
diverges, so does
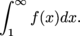
(c) Since
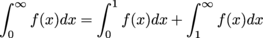
and
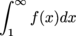
diverges, so does the original integral
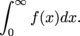
(d) We can't tell what this function does. The function g(x) is less than 
on [0,1), but the integral
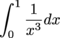
diverges, which doesn't tell us anything. The function g(x) is greater than 
on [0,1), but
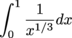
converges, so this doesn't tell us anything either!
(e) We can't tell what
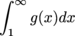
does. Since
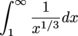
converges, it doesn't help to know that 
on [1,∞).
Since
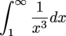
diverges, it doesn't help to know that 
on [1,∞).
(f) We can't tell what
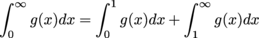
does, because we can't tell if either integral on the right-hand side diverges.
, but since
and
and
doesn't help, because
is the same as the function 
. We know the integral of this function from 0 to 1 converges, and the integral of this function from 1 to ∞ diverges.
and
that doesn't help us at all.
, we can't tell what
and 
converges, does
converge or diverge?
converges or diverges.
, and
converge or diverge?
