Answer
(a)
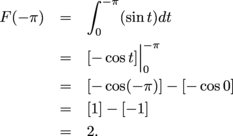
Because we're integrating to the left, this value is the negative of the weighted area between sin t and the t-axis on [-π, 0]. So it's the positive value of this area:
(b)
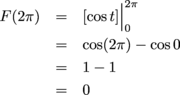
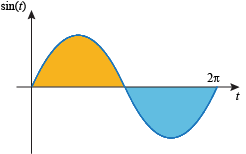
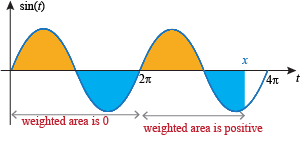
This makes sense, because the weighted areas between sin t and the t-axis on [0, 2π] cancel out:
(c)
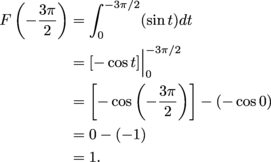
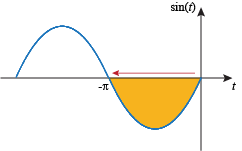
Since we're integrating to the left, this is the negative of the weighted area between sin t and the t-axis on  :
:
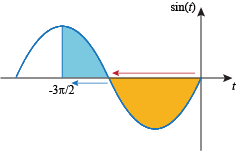
The weighted area on  is zero, because the areas above and below the axis on this interval are equal:
is zero, because the areas above and below the axis on this interval are equal:
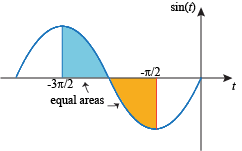
We're left with the negative of the negatively weighted area between sin t and the axis on  , which is this area:
, which is this area:
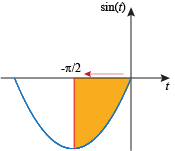
(d) We're integrating starting at 0. When we integrate sin t on the interval [0, 0] we get 0, so
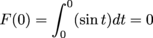
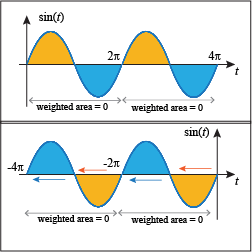
When x is any integer multiple of 2π (positive or negative),
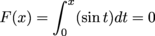
because the weighted areas the integral accumulates cancel each other out:
For any value of x in (0,π], the function
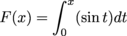
accumulates a positively weighted area, so the value of the function will be positive:
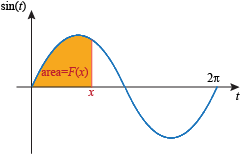
For any value of x in (π, 2π), the area below the t-axis is smaller than the area above the t-axis, so the function
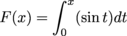
is still positive:
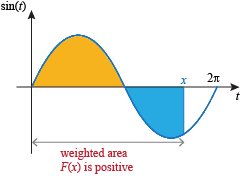
Since  , when we move x into the interval (2π, 3π] the values of F(x) are still positive:
, when we move x into the interval (2π, 3π] the values of F(x) are still positive:
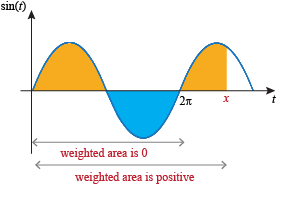
And similarly for x in the interval (3π, 4π):
We can generalize to say that F(x) is zero when x is an integer multiple of 2π and positive for all positive values of x that aren't multiples of 2π.
When x is a negative multiple of 2π, we know that F(x) = 0. What about when x < 0 is not a multiple of 2π?
When x < 0 the function F(x) integrates to the left, so we count areas below the axis positively and areas above the axis negatively.
For x in [-π, 0) the function F(x) counts this area positively. This means F(x) > 0 for x in [-π, 0).
For x in (-2π, -π) the function F(x) considers the area below the axis positively, and the area above the axis negatively. Since there's more area below the axis than above the axis, F(x) is positive.
Generalizing, F(x) will be positive for all x < 0 that aren't multiples of 2π.
Putting all our observations together, we can finally answer the question.
(i) F(x) is positive for all x that aren't multiples of 2π.
(ii) F(x) is never negative.
(iii) F(x) is zero for all x that are multiples of 2π.
In the previous integral we used 0 as the lower limit of integration, but we can build a similar function using any lower limit of integration we want.