Let’s say we’re making an intro for our YouTube movies. Using an online template we have 3 song choices that sync with the template, 4 different colors we can use for our text, and 2 background graphics. How many choices do we have in all?
There are 3 songs to choose from: Jazzel, Funkadoor, and Pipesong. The 4 colors are neon green, silver, banana yellow, and cobalt. Finally, we can either have stars as our background graphics, or swirls. Let’s make a chart to see all of the possible intros. Starting with song choice we get:

No matter which song we pick, we now have 4 colors to choose from.
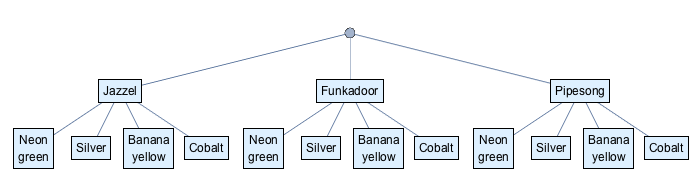
For each of the 4 colors, we have 2 graphics to choose from.

Counting up each final branch on the tree diagram, we see there are 24 possible video intros we can make. Our favorite is Funkadoor, cobalt, swirls.
But if the question is just, “how many different intros can we make?” then the answer is simple to find. We can multiply the number of options for each choice and that gives us the total number of outcomes. So we can multiply 3 × 4 × 2 and see that there are 24 different outcomes. This is called the Counting Principle.
Basic counting principle: to find the total possible outcomes for two or more events, simply multiply the possible outcomes for each event together
Total Outcomes = # of outcomes for event 1 × # of outcomes for event 2 × # of outcomes for event 3, and so on…
Example 1
There are 4 different coins in this piggy bank and 6 colors on this spinner.
If you pick 1 coin and spin the spinner: a) how many possible outcomes could you have? b) what is the probability that you will pick a quarter and spin a green section? |
Example 2
If you spin each of these spinners... a) how many different combined outcomes could you get? b) what is the probability that both spinners land on the same color? |
Example 3
A pizza parlor allows you to choose between thin or thick crust, whole wheat or plain dough, spicy or regular tomato sauce, and four different types of cheese all before you decide on your toppings. a) How many different pizzas can you make from these selections? b) Assuming all options are chosen equally, what is the probability that a thin crust, whole wheat pizza with spicy sauce will be ordered? |
Exercise 1
What is the probability of flipping a coin four times in a row and having it land on heads each time?
Exercise 2
If you are allowed to choose one fruit, one sandwich, and one bag of chips, how many different lunches can be made from these choices: apple, orange, banana, PB&J on whole wheat, turkey and Swiss on sourdough, tuna salad on rye, Fritos, Cheetos, Nacho Cheese Doritos, or Sunchips?
Exercise 3
If you pick one card each from two decks of cards, what is the probability that both cards will be the Ace of Spades?






