Translating spoken-word phrases into algebraic expressions is the start to an awesome session of puzzle-solving. It's like setting up all the pieces before playing a game.
Writing algebraic expressions requires us to read (and re-read) a phrase until we see the math behind each word. That means we need to get at the phrases' values and operations. Once we know the values and the operations we'll be working with, we arrange them in the way the phrase says.
For example, let's translate "4 more than x." To translate this phrase into math, we need to identify more than as our operational words and 4 and x as the two values. Since more than means addition, we know our expression needs to include an addition sign. Now, we just have to arrange things in the right order.
If there's a tricky part to translating spoken-word to math (and we're not saying there is), it's getting everything in the correct order. But the correct order will be right there in the phrase, so it's not tricky.
If we re-read our phrase, "4 more than x," we know that whatever x is, we need 4 more, making the expression x + 4. And that's that.
This is the frustrating part. Since we don't know the value of x (and we don't have a value equivalent to our expression), we stop here. We can't actually solve the expression. That's another lesson.
Tips and Tricks
We've got to be really careful with subtraction. Consider the phrase "8 less than t." We can pick out "less than" as our operational words. "Less than" points to subtraction, but we need to be sure to place the numbers in the correct order since subtraction is tricky. Is 8 – t really 8 less than t? Nope. That's t less than 8. To write "8 less than t," we wanna arrange our expression as t – 8, which truly shows taking away 8 from t.
Let's give the phrase "the quotient of y and 8" a whirl. First, we notice that "quotient" means the answer to a division problem, so our expression needs to include a division sign or a fraction bar:
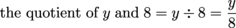
Writing algebraic expressions for multiplication is especially fun because we can be a bit lazy. Suppose we have the phrase "9 times g" or "the product of 9 and g." We know that "times" tells us to multiply, making our phrase 9 × g.
Fun fact: in algebra, when multiplying a number and a letter together, we can squish the number and letter together and skip the multiplication sign. That means simply writing 9g is the same as "9 times g."Man, not having to write that multiplication sign feels so bad…in a good way.
The more anyone practices translating from spoken-word to math, the easier it gets. 100% guaranteed.